Grundläggande hållfasthet och materiallära
Deformation,
skillnaden mellan olika material
Hållfasthet
för armerade härdplaster
Grundläggande hållfasthet och materiallära
När man jämför material med varandra kan man tala om materialens hållfasthetsegenskaper. Det inbegriper generellt hur starkt och styvt materialet är men även mer specifikt hur materialet påverkas då det belastas.
Hållfasthet
Olika material är olika starka. Det innebär att när två provbitar av olika material utsätts för en lika stor belastning, av samma typ och i samma riktning så kan det ena provbiten brista eller deformeras medan den andra provbiten återgår till sin ursprungliga form efter att den har slutat att belastas. Det material som höll har högre hållfasthet vid den specifika belastningen.
Detta betyder dock inte att den provbit som höll har högre hållfasthet vid alla typer av belastningar. Man skiljer därför på hållfasthetsegenskaperna vid olika belastningsfall.
Det förekommer fyra grundbelastningsfall som ett material kan utsättas för:
DRAG
![]()
TRYCK

SKJUVNING

BÖJNING
Utifrån hur mycket belastning en provbit med en specifik tvärsnittsarea klarar innan provbiten brister eller deformeras vid ett visst belastningsfall kan man avgöra materialets hållfasthet vid belastningsfallet. Detta ger grunddata som beskriver hur starkt ett material är vid en viss belastning: draghållfasthet, tryckhållfasthet, skjuvhållfasthet och böjhållfasthet.
Draghållfasthet
Ofta är det enklast att mäta hållfastheten vid belastningsfallet: drag, varvid man får fram draghållfastheten för materialet.
Definition
Man definierar den kraft i Newton [N] som krävs för att dra av eller deformera en provbit med en tvärsnittsarea på en kvadratmeter [m2]. Enheten på dragspänningen (s) är pascal [Pa], ofta med prefixet mega [M], dvs en miljon.
Om det tex krävs en kraft på 200N för att dra av eller deformera en provbit med en tvärsnittsarea på 1mm2, så är materialets draghållfasthet 200MPa:
200[N] / 1*10-6[m2] = 200*106[Pa] = 200[MPa]
E-modul
Alla material är mer eller mindre elastiska. För tex gummi är elasticiteten hög medan den är lägre för stål. Detta innebär att ett gummiband med lika stor tvärsnittsarea som motsvarande stålstång sträcks betydligt längre vid samma belastning. Stål är alltså styvare än gummi.
Måttet på styvheten för ett material kallas elasticitetsmodulen, eller E-modulen för materialet. Stål har alltså högre E-modul än gummi trotts att gummi är mer elastiskt.
På samma sätt som med hållfastheten kan E-modulen beskrivas vid olika belastningsfall: E-modulen vid drag, tryck, skjuv och böjning. Om inget annat anges vid beskrivningen av E-modulen för ett visst material avses vanligtvis E-modulen vid drag.
Definition
Man definierar den dragspänning (s) i pascal [Pa] som krävs för att uppnå en viss töjning (e).
Enheten på E-modulen är pascal [Pa], ofta med prefixet giga [G], dvs en miljard.
Om det tex krävs en kraft på 200 N för att sträcka en provbit med en area på 1mm2 2 procent är materialets E-modulen (drag) 10GPa:
200[N] / 1*10-6[m2] / 0,02 = 100*109[Pa] = 10[GPa]
Deformation, skillnaden mellan olika material
Olika material påverkas på olika sätt då de belastas. Vissa bibehåller sin form ända tills de brister och återgår till sin ursprungliga form om de slutar att belastas innan dess. Detta gäller tex keramer och styva plaster och fiberarmerade plaster. Andra material som metaller och sega plaster deformeras innan brott och återgår då inte till sin ursprungliga form.
Då ett material utsätts för en så stor belastning att den deformeras säger man att den når sin sträckgräns. Då materialet utsätts för så stor belastning att ett brott sker når den sin brottgräns.
Under belastande av ett material är vanligtvis deformationen proportionell mot kraften under den första delen av sträckningen för att sedan minska, vilket sker när man har nått materialets proportionalitetsgräns.
För att ta reda på hur ett material belastas kan man studera ett spänning-töjningsdiagram för materialet.
Spänning-töjningsdiagram tas fram genom att en provbit dras med hjälp av en utrustning som som hela tiden mäter kraften som provbiten utsätts för och hur mycket provbiten töjs medan belastningen av provbiten successivt ökas.
Nedan visas ett typiskt spänning-töjningsdiagram för de vanligaste konstruktionsstålen:
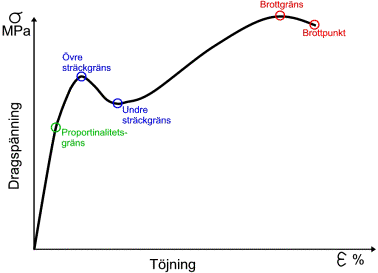
Schematiskt spännings-töjningsdiagram för metaller
För de material där ett brott sker innan att materialet har deformerats talar man om ett sprött brott, späning-töjningsdiagram för ett sådant material, tex styv plast som syns i diagrammet nedan:
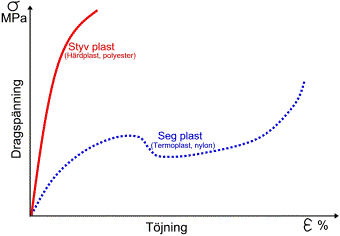
Schematiskt spänning-töjningsdiagram för styv plast respektive seg plast
Även ett exempel spänning-töjningsdiagrammet för en seg plast är plottat i diagrammet (streckad kurva). Kurvan liknar den för mjukt stål, då sega plaster deformeras innan brott (då mikrosprickor uppstår i plastmaterialet), men den stora skillnaden mot metaller är att seg plast saknar proportionalitetsgräns eller någon del på kurvan där en ökad dragspänning ger en proportionellt ökad töjning.
Hållfasthet för armerade härdplaster
Eftersom armerade härdplaster är kompositer där olika material med olika egenskaper samverkar är hållfasthetsegenskaperna annorlunda än för homogena material som metaller eller oarmerad plast.
Egenskaperna hos materialet påverkas av plastens mekaniska egenskaper, fibrernas egenskaper, hur plasten binder samman fibrerna och hur fibrerna är fördelade, deras riktning i materialet, längden på de ingående fibrerna osv. De många faktorerna gör beräkningar av hållfastheten hos en konstruktion av fiberarmerad plast ofta betydligt mer komplex än beräkningarna för en konstruktion av ett homogent material.
I många fall genomförs därför inga regelrätta hållfasthetsberäkningar då privatpersoner eller mindre industrier tar fram enstaka konstruktioner i fiberarmerad plast. Dock krävs att konstruktören har ett ”hum” om hur materialet fungerar och påverkas beroende på de olika faktorerna för han eller hon skall kunna ta fram någorlunda optimerade konstruktioner i fiberarmerad plast utifrån de förutsättningar som finns.
Dragbelastning
Om en fiberarmerad härdplast utsätts för dragande belastning styrs materialets draghållfasthetsegenskaper främst av fibrernas hållfasthetsegenskaper, eftersom fibrernas draghållfasthet är betydligt högre än härdplastens.
Vid dragande belastning är töjningen relativt proportionell mot belastningen ända tills den armerade härdplasten tvärt går av.
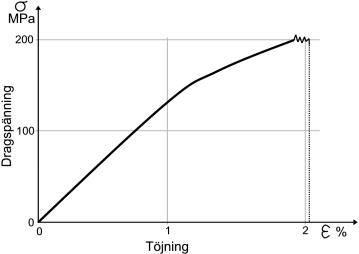
Typiskt spänning-töjningsdiagram för en fiberarmerad härdplast. Observera knäcken, delar av fibrerna kan nu ha gått av, bindning mellan fibrerna och matrisplasten kan ha försämrats eller mikrosprickor i matrisplasten kan ha uppkommit.
E-modulen (drag) kan därför med relativt stor säkerhet beräknas genom att draghållfastheten divideras med materialets töjning vid brott.
Genom att
studera spänning-töjningsdiagram där töjningen och spänning fram till brott
bildar en linjär kurva kan man bedöma armeringsplastens E-modul (drag), detta
genom att studera kurvans lutning. En brantare kurva innebär en högre E-modul
för materialet.
I spänning-töjningsdiagrammet nedan kan man se kurvor för två material med samma draghållfasthet (1000MPa) men olika töjning vid brott (2% respektive 4 %).
E-modulen (drag) för dessa material är alltså 50 GPa respektive 25 GPa:
1000*106[Pa]
/ 0,02 = 50*109[Pa]
= 50[GPa]
1000*106[Pa] / 0,04 = 25*109[Pa] = 25[GPa]
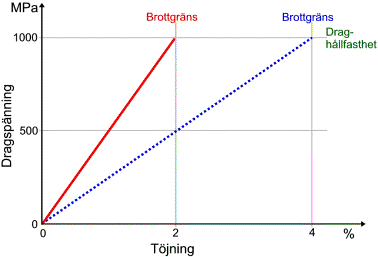
Förenklat spänning-töjningsdiagram för två kompositer med samma draghållfasthet men olika töjning vid brott, (typiska kurvor för längsriktat laminat med kolfiber respektive glasfiber)
Tryckbelastning
Rena armeringsfibrerna kan bara ta upp ren dragande belastning och det är först efter att de har bundits samman av härdplasten som de även kan ta upp den motsatta belastningen dvs tryckande belastning.
Vid tryckbelastning av en fiberarmerad plast styrs hållfasthetsegenskaperna både av fibrernas hållfasthetsegenskaper men även till stor del av plastens möjlighet att binda samman fibrerna och plastens egna hållfasthetsegenskaper.
Trycket påverkar den fiberarmerade plasten så att fibrerna tvingas bukta och pressas isär medan plasten både pressas samman och dras isär.
Då man teoretisk skall beräkna tryckhållfastheten för en fiberarmerad härdplast måste man se till en rad faktorer, som bla fiberns draghållfasthet, plastens bindning mot fibrerna och den rena plastens tryck- och draghållfasthet. Dessutom ändras vissa faktorer från fall till fall, bla hur väl plasten binder fibrerna men även plastens mekaniska egenskaper, beroende på hur lamineringen och härdningen har gått till samt vilken aktuell temperatur som materialet utsätts för.
Detta gör teoretiska beräkningar av tryckhållfastheten hos en fiberarmerad härdplast komplexa och inte helt tillförlitliga.
Skjuvbelastning
Vid skjuvbelastning av en fiberarmerad härdplast tvingas fibrerna glida gentemot varandra. Detta gäller speciellt om skjuvbelastningen påverkar ett traditionellt fiberlaminat (flerlagerskomposit) där fibrerna sitter i lager.
Plastens bindande egenskaper av fibrerna samt plastens direkta skjuvhållfasthetsegenskaper styr till största del laminatets totala skjuvhållfasthet.
För att beskriva bindningsstyrkan hos plasten samt armeringsfibrernas möjlighet att bindas av plasten i ett fiberlaminat mäts bla något som kallas ILSS (interlaminar shear strength) vilket ger ett mått på laminatets spjälkhållfasthet längs laminatet.
Liksom för tryckbelastning är det komplicerat att beräkna skjuvhållfastheten teoretiskt för en fiberarmerad härdplast och hur en konstruktion av armerad härdplast påverkas exakt vid skjuvande belastning. Beroende på bla lamineringsmetoden och omgivande temperatur är det inte heller säkert att teoretiska beräkningar blir tillförlitliga.
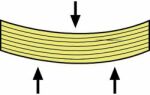
Böjbelastning
 Vid
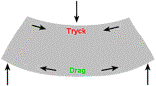
böjande belastning av tex en balk som i den schematiska figuren till vänster
uppstår en kombination av tre belastningsfall: tryckbelastning på ovansidan,
dragande belastning på undersidan och skjuvbelastning mellan balkens övre del
och undre del.
Vid
böjande belastning av tex en balk som i den schematiska figuren till vänster
uppstår en kombination av tre belastningsfall: tryckbelastning på ovansidan,
dragande belastning på undersidan och skjuvbelastning mellan balkens övre del
och undre del.
I en fiberarmerad plast gör kombinationen av belastningarna att den fiberarmerade plastens totala böjhållfasthet både beror på fibrernas och plastens hållfasthetsegenskaper, plastens möjlighet att binda fibrerna, men även fibrernas mängd, riktning och längd i kompositen.
I en homogen balk ökar böjstyvheten med kubiken av tjockleksökningen på balken.
En dubbelt så tjock balk ger alltså 8 ggr så hög böjstyvhet (23 = 8) medan böjstyheten ökar med 27 gånger om balken är tre gånger så tjock (33 = 27).
I en homogen balk ökar böjhållfastheten för balken med kvadraten av tjockleksökningen.
En dubbelt så tjock balk är alltså 4ggr så stark (22 = 4) medan en tre gånger så tjock balk är 9 ggr så stark (32 = 9).
Vid andra former (cylindrisk, rör mm) påverkas böjstyvheten och böjhållfastheten annorlunda med ökade dimensioner, se facklitteratur tex Karlebo handbok.
Det finns många ytterligare hållfasthetsbegrepp och det går fördjupa sig nästan hur mycket som helst men för att konstruera i fiberarmerad härdplast på hobbybasis eller mindre industriell skala där kraven inte är så höga, där det inte finns några krav på en optimal konstruktion med maximal styrka och styvhet, minimal vikt och materialåtgång osv krävs ofta inte mer än goda grundkunskaper och sunt förnuft!